I am Hongda Qiu, a fifth year Ph.D. student in Mathematics at The Pennsylvania State University. My advisors are Prof. Dmitri Burago and Prof. Anton Petrunin. Before that, I obtained my Bachelor of Science in Mathematics and Applied Mathematics at Zhejiang University, Hangzhou, China in 2018 and my M.S. in Applied Mathematics and Stateistics in Johns Hopkins University. Here is my CV.

My email is hqiu[at]psu[dot]edu

For Academics: Publications

For undergraduate students at PSU: Teaching

For those intrigued by math like myself: Mathematical Assets

Reseach Interests

I am interested in differential geometry and Riemannian geometry, and their interaction with topology and group theory. One of the themes in my thesis research is the geometry of isometric embeddings. Namely, I study whether isometric embeddings of (non-compact) Riemannian manifolds can be constructed to preserve symmetries. A classical result is Mostow’s embedding theorem of compact manifolds acted upon by a Lie group, but the study on non-compact manifolds is settled down in higher generality. There are also open problems related to algebra, such as whether certain types of discrete groups (i.e. the Heisenberg group $\mathbb{H}^3$ can act by isometries on (some higher-dimensional) Euclidean spaces.

Another topic is about the relation between topology and ambient geometry. This appears to be an unexplored area after the classical results on the maximal imbedded ball problem by Pestov and Ionin in the plane and by Lagunov and Fet in $n$-dimensional case. For instance, given a closed surface in $\mathbb{R}^3$ with bounded principal curvatures, what can we say about its enclosed volume? Does such a surface necessarily enclose a ball of some radius? There are many open problems, even in the three dimensional case. Besides geometry, one might also get intrigued by the topology flavors of this area. For instance, the classification of bodies bounded by closed surfaces in $\mathbb{R}^3$ still remains open.

Impacted by my advisor Dmitri Burago and many other people at PSU, I also pay some of my attention to the interconnection between dynamical systems and geometry. There are two areas closely related to non-positively curved spaces: the billiards and the ergodicity of geodesic flows. The geometrical aspect motivates enough discussion. For instance, the ergodicity of geodesic flows on a non-positively curved surface of genus $\geq 2$ has been partially proved by Wu (the Katok conjecture), but no one knows how the general case resolved. However, recently, there is a hope to push forward by studying the geometry of flat geodesics on a Hadamard space.

Publications

Supersqueezed surface: a counterexample for the curvature bounded sphere problem in $\mathbb{R}^3$, Submitted, 2025

For 3D models about this work, see Mathematical Assets

On equivariant isometric embeddings of Riemannian manifolds with symmetries. https://arxiv.org/abs/2511.09931, Submitted, 2025

With Dmitri Burago. On the geometry of Riemannian isometric embeddings. https://arxiv.org/abs/2507.23164, Submitted, 2025

On the curvature bounded sphere problem in $\mathbb{R}^3$. https://arxiv.org/abs/2507.06245, Submitted 2025

With Dmitri Burago. Dong Chen and Jinpeng Lu, On some unsolved problems of geometric origin. Preprint, 2024

Teaching

Fall 2025 MATH 022 College Algebra Lecture_notes

Spring 2023 MATH 035 General Views on Mathematics Course_page

Spring 2022 MATH 230 Calculus III Lecture_notes

Mathematical Assets

Lagunov’s Fishbowls

These are smooth closed surfaces of genus $2$ with bounded principle curvatures but have very ``crowded” interior. Namely, the maximal ball can be embedded in them are very small.

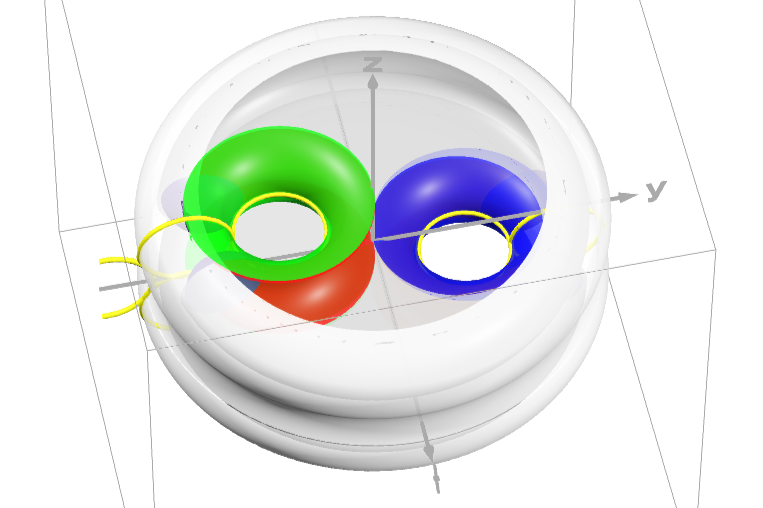
The oringal 3D model is here: Lagunov’s Fishbowl

Anton Petrunin suggested an engineering improvement to further squeeze its enclosed volume.

Supersqueezed spheres

These are smooth topological spheres in $\mathbb{R}^3$ with $|k_n|\leq1$ but small enclosed volumes ($<4<4\pi/3$).

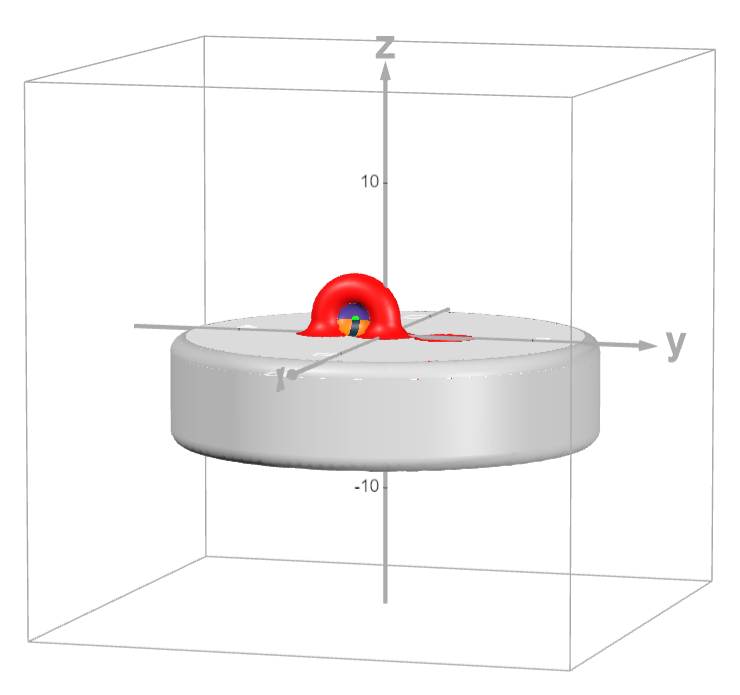
The oringal 3D model is here: Supersqueezed sphere

And here is a more twisted one

Miscellaneous

Out of math, I am a pianoist keen on both classics and Jazz. My favorite composers are Chopin, Xinghai Xian and Oscar Peterson.

I play piano and digital piano for the Asian Classical Music Club at PSU.

An April Fool Day’s Joke I played with many people in academics